伟大的数学家们是在多大的时候改变的世界?
英国数学家戈弗雷・哈罗德・哈代 (G.H. Hardy) 有一句名言:"... 比起其他艺术或者科学,数学更像一个年轻人的游戏。”这里,他对" 年轻人 " 的理解有多正确呢?
诚然,证明一个数学定理需要大量的创造力、重新认识问题的能力,还要用其他人没有想到的方式来进行思考。
但,它也需要大量的经验和知识储备。毕竟,如果不理解一个问题,你也就无法证明它。很多未经证实的猜想都建立在一座概念堆积的山峰之上,登顶往往需要数年。
基于维基百科,我列出了 1501~2015 年数学发展的时间线,追溯了 250 件数学领域的大事:定理的新证明、重要工作的发布,或者核心数学概念的萌芽。
以下是其中的一些事件:
1540 年,18 岁的洛多维科・费拉里 (Lodovico Ferrari) 解出了四次方程。
1799 年,22 岁的卡尔・弗里德里希・高斯 (Carl Friedrich Gauss) 证明了代数的基本定理(每个多项式方程在复数中都有一个解)。
1925 年,24 岁的维尔纳・海森堡 (Werner Heisenberg) 和约尔当 (Jordan)、 玻恩 (Born) 建立了量子力学的矩阵表示。
2004 年,29 岁的陶哲轩 (Terence Tao) 和本・格林 (Ben Green) 证明了格林-陶定理 (Green–Tao theorem)。
1522 年,30 岁的亚当・里斯 (Adam Ries) 解释了阿拉伯数字的使用及其相对于罗马数字的优势。
2003 年,37 岁的格里高利・佩雷尔曼 (Grigori Perelman) 证明了庞加莱猜想。
1994 年,41 岁的安德鲁・怀尔斯 (Andrew Wiles) 证明了谷山志村猜想的一部分,从而证明了费马大定理。
1929 年,47 岁的艾米・诺特 (Emmy Noether) 首次引入了群和代数的通用的表示理论。
2013 年,58 岁的张益唐证明了存在无穷多对间隙为有限的质数。
1618 年,68 岁的约翰・纳皮尔 (John Napier) 在一部关于对数的著作中首次提到了自然对数的底数 e。

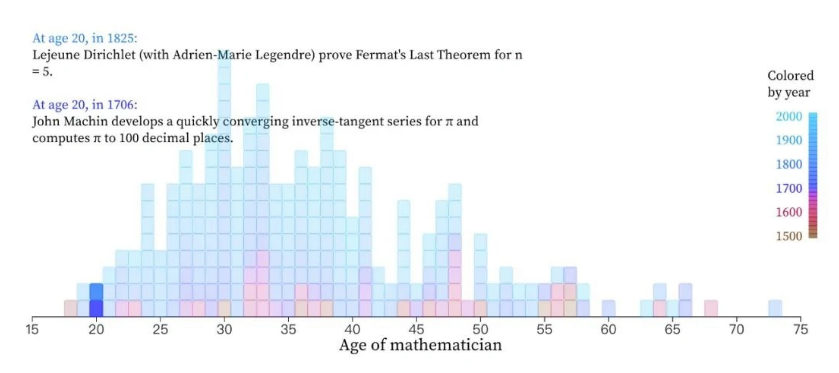
伟大数学家们的年龄
数据汇总:
Ø 他们的平均年龄为 37 岁;
Ø 年龄的中位数略低,为 35 岁;
Ø 数学大事记中 25 % 的数学家们在他们 30 岁以下做出了重要的数学成果;
Ø 42 % 的数学家在 30-39 岁之间做出了重要的成果;
Ø 33 % 的数学家在 40 岁或者以上做出了重要的成果;
Ø 其中最小的年龄是 18 岁,1540 年洛多维科・费拉里 (Lodovico Ferrari) 推导出了四次方程的一般解;
Ø 最大的是 73 岁,1825 年阿德里安-马里・勒让德 (Adrien-Marie Legendre) 和约翰・彼得・古斯塔夫・勒热纳・狄利克雷 (Peter Gustav Lejeune Dirichlet) 一起证明了对于 n=5 情况下的费马大定理。
从 20 岁到 70 岁
我做了一个交互式的图表《伟大的数学家时代》,读者可以点击这里或下图来获取详细的信息(使用滑块来调查各个年龄段的数学家们的成就)。其中有一些亮点值得注意:
在 20 岁到 29 岁之间
1832 年,法国数学家埃瓦里斯特・伽罗瓦 (Évariste Galois) 在他 21 岁时提出了代数方程可解性的一般条件,因此基本建立了群论和伽罗瓦理论,他也是第一个使用“群”这一个数学术语来表示一组置换的人,与尼尔斯・阿贝尔并称为现代群论的创始人。但充满悲剧和传奇色彩的是,在他提出这些理论不久,就在一场决斗中被杀。
1913 年,年仅 26 岁的印度数学家斯里尼瓦瑟・拉马努金 (Srinivasa Ramanujan) 给哈代写了一封信,信上是一长串没有证明的定理,在信里,拉马努金同时恳请哈代帮他摆脱贫困的现状。当然,拉马努金在信中的发现一定早于他 26 岁之前。
在 30 岁到 39 岁之间
2008 年,伊朗德黑兰数学家玛丽安・米尔札哈尼在她 31 岁时证明了一个长期以来没有解决的猜想:威廉・瑟斯顿 (William Thurston) 提出,泰希米勒空间 (Teichmüller) 上的地震流 (Earthquake map flow) 都是遍历系统。六年后,她被授予菲尔兹奖,以表彰她 "对黎曼曲面及其模空间下的动力学和几何学的杰出贡献"。2017 年 7 月 14 日,米尔札哈尼因乳腺癌去世,终年 40 岁。
1837 年,32 岁的德国数学家约翰・彼得・古斯塔夫・勒热纳・狄利克雷 (Gustav Lejeune Dirichlet) 在一篇关于给定算术级数中存在素数的论文中发展了解析数论。这是狄利克雷在数学时间线上的第四个工作,前三件工作分别在他 20 岁,27 岁和 32 岁时发生。
1915 年。36 岁的理论物理学家阿尔伯特・爱因斯发表了他的广义相对论,十年前,他的狭义相对论发表,当时他还是瑞士专利局的职员。
在 40 岁到 49 岁之间
1993 年,在秘密研究费马大定理几年之后,40 岁的安德鲁・怀尔斯 (Andrew Wiles) 宣布证明了费马大定理。众所周知,在审查的过程中,该证明中存在错误,但在次年,该错误被纠正。怀尔斯在 46 岁时扩展了他的工作,完成了谷山志村 (Taniyama Shimura) 全部的猜想。
1918 年,41 岁的戈弗雷・哈罗德・哈代 (G.H. Hardy) 和斯里尼瓦瑟・拉马努金 (Srinivasa Ramanujan) 一起为分割函数开发了一个渐近公式。也许他与年轻的创意天才拉马努金的合作是他哀叹数学是 "年轻人的游戏" 的原因之一。
50 岁以上
2013 年,美籍华裔数学家张益唐首次证明了存在无穷多对间隙为有限的质数,从而在孪生素数猜想这一数论难题上取得质的突破。1991 年张益唐获得博士学位之后未拿到导师的推荐信,学术道路坎坷,有段时间靠打杂来糊口过日,曾经做过几年会计师,在地铁的快餐店打过工。(来源)
1722 年,法国数学家亚伯拉罕・棣莫弗 (Abraham de Moivre) 将复数和三角学联系起来,提出了棣莫弗公式;66 岁时,引入了正态分布来近似二项分布。
关于这位年迈的数学家,有一则幽默轶事:
人们常说,一直对数列感兴趣的棣莫弗曾经预言,他每天需要比前一天多睡 15 分钟,当睡眠总数达到 24 小时的时候,他就会死亡,这个时间是 1754 年 11 月 27 日,这也正是他死亡的时间。(来源)
数据和方法
大部分数据是从维基百科上的数学时间线获得的,从 "现代"(16 世纪) 开始。如果能从古希腊时代的阿基米德 (Archimedes) 和希帕蒂娅 (Hypatia) 开始,那就太好了,但历史记录不够精确,所以这里从“现代”开始。
我还用其他一些著名的结果扩充了维基百科时间轴上提供的数据,例如爱因斯坦,玻尔和海森堡等数学物理学家的工作。
令人惊讶的是,最近数学界的一些的大事件也存在一些数据收集问题。我想包括黄浩(Hao Huang,音译)2019 年对布尔函数的灵敏度猜想的证明,但我找不到他的出生日期。从他的教育经历推断,他可能已经 30 多岁了。
同样,我想把琼・泰勒 (Joan Taylor) 包括在内,她是一位业余数学家,与约书亚・索科拉尔 (Joshua Socolar) 一起发现了索科拉尔-泰勒 (Socolar-Taylor) 瓷砖拼贴,解决了罗杰・彭罗斯 (Roger Penrose) 提出的问题。但我找不到她的出生日期,但在她的网站上,她说她从 1990 年开始思考这个问题,比 2011 年发表的结果早了 20 年。
最后的思考
从统计数据来看,虽然大多数令人瞩目的成就是数学家们在 20 至 40 岁之间取得的,但这个年龄范围仍然很广。随着年龄的增大,数学家们倾向于书籍和概要类型的成果,当然,仍然有一些老数学家们做出的突破性创新证明的例子。
每个数学家的故事都是不同的。这其中,有英年早逝的神童,有覆盖各个领域的多产博学者,还有坚持钻研一个问题 20 年的人。
对于我们这些业余数学爱好者来说,我们也许并不想改变世界,而只是乐于了解它,知道我们的大脑一直在思考,可以继续享受数学带来的快乐,这一点就足以令人开心了。

